Grundkurs Fluidmechanik
oder von Bechern, Flaschen und Menschen?
Fluide sind Fluide sind Fluide
Bei der Behandlung von Hydrocephalus kommt man nicht umhin, sich mit der Beschaffenheit und den Eigenarten von Fluiden zu beschäftigen. Der Liquor cerebrospinalis folgt wie alle anderen Fluide ganz bestimmten Gesetzen der Physik, die es sich lohnt zu verstehen, wenn man dieses Fluid ableiten möchte oder muss.
mehr lesenVon Bechern, Flaschen und Menschen
Bei der Behandlung von Hydrocephalus kommt man nicht umhin, sich mit der Beschaffenheit und den Eigenarten von Fluiden unter Einfluss der Schwerkraft zu beschäftigen. Der Liquor cerebrospinalis (CSF) folgt wie alle anderen Fluide erst einmal ganz bestimmten Gesetzen der Physik, die es sich lohnt zu verstehen, wenn man dieses Fluid ableiten möchte oder muss.
Spätestens mit einem künstlich geschaffenen Kanal - dem implantierten Shuntsystem - zwischen den Hirnkammern und dem Bauchraum wird es kompliziert. Themenfelder wie Hydrostatik und Hydrodynamik werden relevant und können den Erfolg der Hydrocephalustherapie maßgeblich beeinflussen. Was passiert mit den Druckverhältnissen in Flaschen, Bechern und Menschen, wenn sich die Lagen ändern, wenn die Flasche umfällt, sich der Mensch hinlegt, wenn künstliche Ableitungen hinzukommen? Und wieso sind Flaschen und Becher ein beliebtes Modell um den sogenannten "Syphon-Effekt" und die Konsequenzen von Überdrainage zu demonstrieren? Darauf soll dieser Artikel Antworten geben.
Hydrostatik im Shuntsystem
Was haben denn nun Menschen, Flaschen und Becher gemeinsam? Die Unterschiede sind auf den ersten Blick einfacher zu definieren. Wir werden jedoch sehen, dass die beiden letztgenannten durchaus extreme Vereinfachungen von Menschen sein können, wenn man aus einem bestimmten Blickwinkel drauf schaut: Anhand von Flaschen und Bechern lassen sich simple Modelle erstellen, die uns dabei helfen können, grundlegende hydrostatische Effekte im menschlichen Körper zu verstehen.

Zunächst einmal sollten wir jedoch definieren, was genau gemeint ist, wenn wir vor dem Hintergrund der Fluidmechnik von Bechern, Flaschen und Menschen sprechen:
Becher stehen hier stellvertretend für offene Behälter für Wasser oder andere Flüssigkeiten MIT unmittelbarem Kontakt der Flüssigkeit zur sie umgebenden Atmosphäre. Der Druck an der "freien Oberfläche" der Flüssigkeit im Becher ist also bekannt und entspricht dem vorherrschenden Atmosphärendruck.
Eine Flasche ist in diesem Zusammenhang ein allseitig geschlossener, starrer Behälter für Flüssigkeiten – OHNE Kontakt der Flüssigkeit zur sie umgebenden Atmosphäre. Der Flüssigkeitsdruck an der "freien Oberfläche" der Flüssigkeit in der Flasche wurde beim Verschließen der Flasche "eingefroren" und ist von außen nicht mehr ersichtlich.
Menschen stellen – philosophisch und physikalisch – auch eine Art Behälter dar: für Gedanken, Organe und allerlei Arten von Fluiden. Es zirkuliert Luft in unseren Lungen, Blut durch unsere Venen und Liquor cerebrospinalis (CSF) durch unser Hirnkammersystem.
FLUID
Der Begriff Fluid bezeichnet eine Substanz, die - im Gegensatz zu Festkörpern - äußeren Kräften keinen Widerstand entgegensetzt, sondern sich unter Einfluss von externen Kräften kontinuierlich verformen lässt.
Geht mit dieser erzwungenen Formänderung keine Volumenänderung einher - lässt sich das Fluid also nicht komprimieren - dann spricht man gemeinhin von einer Flüssigkeit, wie etwa bei Wasser - oder eben auch beim Liquor cerebrospinalis.
Wir werden sehen, dass der Mensch in diesem Zusammenhang mehr einer geschlossenen Flasche als einem zur Umgebung offenen Becher gleicht, dazu aber später mehr. Widmen wir uns zunächst dem Wasser in unserem Hirnkammersystem - dem Liquor cerebrospinalis:
Der Liquor cerebrospinalis (kurz: CSF, aus dem Engl.: cerebrospinal fluid) ist eine klare, wasserähnliche Flüssigkeit, die überwiegend aus Blutplasma mit nur geringem Anteil an zellulären Bestandteilen – davon überwiegend Lymphozyten, aber auch Protein und Albumin - besteht. Er wird aus dem arteriellen Blutkreislauf im Inneren des Gehirns, hauptsächlich in den Plexus Choroidei, gebildet und – nach heutigem Kenntnisstand – unter anderem in den Granulationes arachnoideae wieder resorbiert.
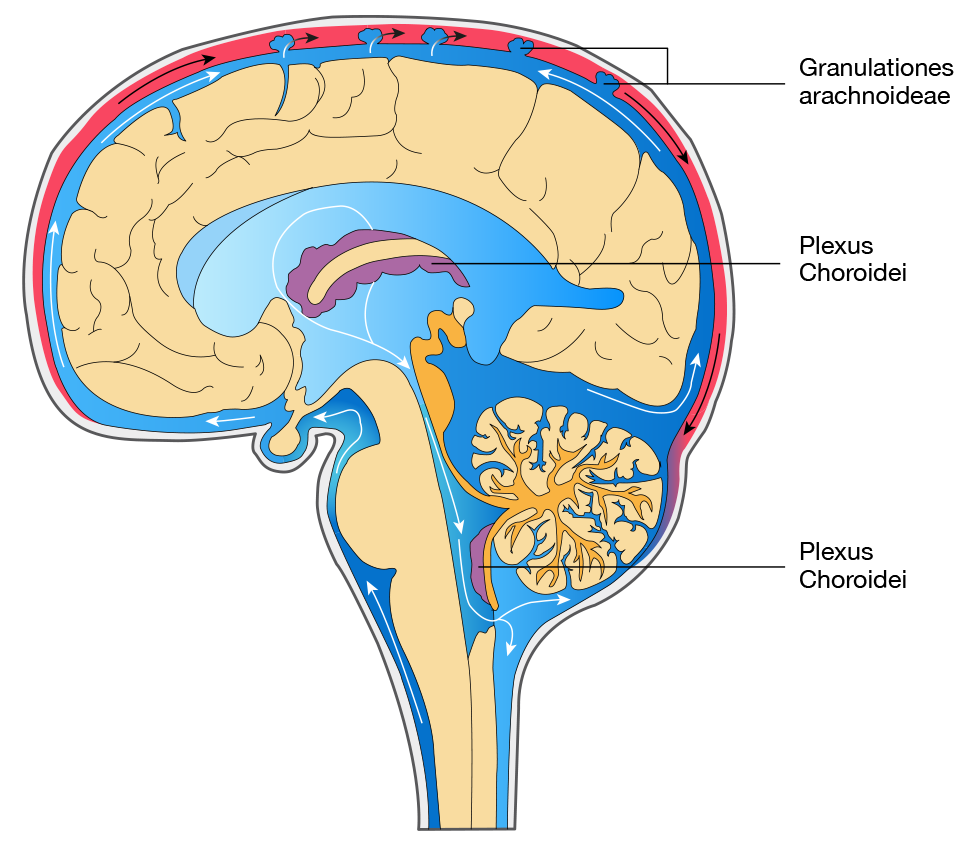
Der Mensch beherbergt zu jeder Zeit ca. 100 – 200 ml CSF in seinem Hirnkammersystem und Spinalkanal. Da ein gesunder Mensch etwa 500 ml der Flüssigkeit am Tag produziert, wird das Gesamtvolumen an CSF im menschlichen Körper täglich mehrfach ausgetauscht – Ventrikel und Spinalkanal werden regelrecht durchspült.
Die Funktionen des CSF sind vielfältig und zum Teil noch Gegenstand der aktuellen Forschung. Unter anderem soll er das zentrale Nervensystem des menschlichen Körpers vor Stößen sowie Druck von außen schützen. Er erfüllt durch seine zellulären Bestandteile immunologische Aufgaben, sorgt für die Entgiftung des Gehirns durch Aufnahme und Abfuhr von Stoffwechselendprodukten und fängt durch statischen Auftrieb einen Teil des Gewichts des Gehirns ab.
AUFTRIEB
Auftrieb bezeichnet ein grundlegendes fluidmechanisches Phänomen, bei dem ein Körper in einem Fluid, entgegen der äußerlich wirkenden Schwerkraft eine Kraft erfährt: wie zum Beispiel Schiffe im Wasser oder das menschliche Gehirn im CSF. Gemäß dem Archimedischen Prinzip entspricht die Auftriebskraft der Gewichtskraft der Menge an Flüssigkeit, die dieser Körper in der Flüssigkeit verdrängt: Das Gewicht des verdrängten Wassers durch ein im Meer treibendes Schiff „drückt“ das Schiff nach „oben“.
Die Ursache des Auftriebs liegt in der Natur von ruhenden Flüssigkeiten im Schwerefeld der Erde - genauer noch: in den dabei in der Flüssigkeit vorherrschenden Drücken. Das wissenschaftliche Teilgebiet, das sich mit den darauf entstehenden Phänomenen auseinandersetzt, wird Hydrostatik genannt.
Physikalisch ist Druck ganz allgemein als „Kraft-pro-Fläche“ definiert. Man erzeugt einen Druck p, indem man eine physische Kraft F auf die Oberfläche eines Festkörpers oder eines Fluids ausübt: im Fall des Fluids herrscht dann bei Vernachlässigung der Schwerkraft überall gleichmäßig der Druck p = F/A. Ein gutes Beispiel ist ein Luftballon, in den Gas oder Wasser mit einer Kraft F gegen die Spannung der Ballonhülle eingedrückt wurde. Im Vergleich zur ihn umgebenden Atmosphäre herrscht im Ballon dann ein Überdruck.
Im Schädelinneren kann ebenfalls ein Überdruck (Hydrocephalus) entstehen – und zwar durch die bereits erwähnte „Raumforderung“, z.B. durch ein übermäßiges Aufstauen von CSF, oder eine Blutung oder eine wachsende Geschwulst. Die notwendige Kraft wird durch deren Ausdehnung oder deren Wachstum erzeugt.
Beziehen wir jetzt auch die Schwerkraft in unsere Betrachtung mit ein, tritt zusätzlich dazu eine besondere Form des Druckes auf, der sogenannte hydrostatische Druck, der durch das Eigengewicht des Fluids entsteht. Dieses Phänomen wird als grundlegende Gesetzmäßigkeit der Hydrostatik - in der Physik bekannt als die Grundgleichung der Hydrostatik – bezeichnet. Diese Gesetzmäßigkeit ist essentiell, um zu verstehen, warum es in einem Shunt abhängig von der Körperlage zu Druckunterschieden in den Ventrikeln und im Bauchraum kommt, warum die Ventrikel im ungünstigsten Fall sogar regelrecht leergesaugt werden können und wie man das verhindern kann.
In möglichst einfachen Worten ausgedrückt, lässt sich das wie folgt umschreiben: Da jede Flüssigkeit auch eine Masse hat – und diese im Schwerefeld der Erde eine Gewichtskraft erfährt – nimmt die Last auf einen sich in der Flüssigkeit befindenden imaginären Körper ausgehend von der "freien Oberfläche" – also der Grenzfläche zwischen der Flüssigkeit und der sie umgebenden Atmosphäre, in der ein uns bekannter (Luft-)Druck herrscht – mit zunehmender Tiefe gleichmäßig zu. Der dabei entstehende Flüssigkeitsdruck hängt ausschließlich von der Höhe der darüber liegenden Flüssigkeitssäule, nicht jedoch von der Form des Gefäßes und somit der Masse der Flüssigkeit über dem betrachteten Ort ab.
Ein gutes Beispiel ist ein mit Wasser gefüllter (beliebig geformter!) Becher: im Unterschied zum Ballon muss das Wasser nicht mit einer besonderen Kraft in das Glas gedrückt, sondern kann einfach eingefüllt werden. Auf der Wasseroberfläche herrscht natürlich immer der Umgebungsdruck, d.h. der Atmosphärendruck (je nach Wetterlage ca. 1 bar). Unten im Becher herrscht derselbe Umgebungsdruck, aber zusätzlich lastet noch das gesamte Gewicht der Wassersäule (nicht des gesamten Wassers!) über dem Glasboden. Letzteres erzeugt einen Zusatzdruck, den anfangs benannten hydrostatischen Druck. Dieser nimmt von „Null“ an der Wasseroberfläche bis zu einem Maximum zu, je tiefer man von oben startend nach unten in das Wasser eintaucht, einfach weil immer mehr Wassergewicht über der Ebene lastet, in der man den Druck betrachtet.
GRUNDGLEICHUNG DER HYDROSTATIK
Für Experten und Rechenbegeisterte: Der hydrostatische Druck lässt sich sehr einfach herleiten. Hierfür benötigt man nur einige einfache physikalische Basisformeln:
(1) Druck = Kraft/Fläche;
p = F/A (allgemeine Definition)
(2) Hydrostatischer Druck = Gewichtskraft/Fläche;
pHD = G/A (spezielle Definition)
(3) Gewichtskraft = Masse * Konstante; G = M * const.
(M Masse des Körpers in g oder kg, const./Naturkonstante)
(4) Dichte = Masse/Volumen; d = M/V
(Dichte d für Wasser: d = ca. 1 g/cm3/ Materialkonstante)
Aus Gleichung (4) ergibt sich die Masse des Wassers:
M = d * V (5).
Das Volumen des "Wasserzylinders" im Falle des Wasserglases ergibt sich aus dem folgenden Bild zu V = h * A (6), wobei A die Grundfläche des Glases und h die Höhe des Wasserspiegels im Glas ist: siehe Abbildung rechts
(6) in (5) eingesetzt ergibt:
M = d * V = d* h* A (7)
Der hydrostatische Druck nach (2) ist also mit (3) und (7):
pHD = G/A = M*const./A = d*h*A*const./A (8).
Durch Vereinfachung kommen wir schließlich zur hydrostatischen Grundgleichung:
pHD = d* const.*h (9).
Es wird deutlich, dass der hydrostatische Druck (außer von der Dichte d der Flüssigkeit) nur und ausschließlich von der Höhe h der Flüssigkeitssäule abhängt.


Hydrostatisches Paradoxon
Da dieser Sachverhalt auf den ersten Blick zunächst nicht intuitiv erscheint, spricht man in diesem Zusammenhang auch vom sogenannten hydrostatischen Paradoxon.
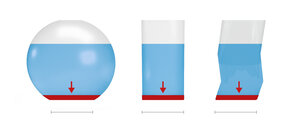
Aus der alltäglichen Erfahrung kennen wir es alle: Ob wir 10 Meter tief im Becken eines Schwimmbads oder 10 Meter tief im Ozean tauchen, ist für den Druck, den wir dabei in unseren Ohren spüren, unerheblich.
Hydrostatischer Druck ist also ausschließlich von der Tiefe abhängig.
HYDROSTATISCHER DRUCK IN cmH2O
Der Druck im Liquor cerebrospinalis wird im medizinischen Fachjargon in der nicht-SI-Einheit („SI“ steht dabei für Système international d’unités und bezeichnet das internationale Einheitssystem für physikalische Größen) cmH2O ausgedrückt - gesprochen: „Zentimeter-Wassersäule“. Es ist ein sogenannter Differenzdruck, der den Druckunterschied (d.h. die Druckdifferenz) zwischen Schädelinnerem und äußerem Luftdruck beschreibt.
Ein cmH2O ist definiert als der hydrostatische Druck, den eine Wassersäule von einem Zentimeter Höhe bei einer Dichte von exakt einem Gramm pro Kubikzentimeter Wasser bewirkt. Anders als bei der für Druck üblichen Einheit Pa - gesprochen: „Pascal“ - die definiert ist als die Kraft eines Newtons, die auf eine Fläche von einem Quadratmeter wirkt, handelt es sich bei der Einheit cmH2O um eine Größe, die ganz ohne Wirkfläche auskommt. Sie bezieht sich lediglich auf ein eindimensionales Längenmaß, nämlich die Höhe der Wassersäule, die auf dem betrachteten Druckpunkt lastet. Dies entspricht nicht unserem intuitiven Verständnis von Druck, verdeutlicht dafür jedoch umso mehr die Wirkung des hydrostatischen Drucks – also dem Druck in einem Medium (z.B. in einer Flüssigkeit), der durch das Eigengewicht dieses Mediums selbst hervorgerufen wird. In anderen Worten: der Druck entsteht, weil das Medium mit seinem eigenen Gewicht auf sich selber drückt.
Ein cmH2O entspricht in etwa einem Millibar oder in SI-Einheiten ausgedrückt: tausend Pascal.
Der Hydrostatische Druck wird nach der Formel
HSP = rho * g * h
berechnet. Dabei ist h die Höhe der Flüssigkeitssäule und rho und g physikalische Konstanten.
Früher wurde als Flüssigkeitssäule auch gerne Quecksilber verwendet, das viel schwerer als Wasser ist: 1 mm Quecksilber (1 mmHg , auch Torr genannt) erzeugt ungefähr denselben Druck wie 1,36 cm Wasser. Gerade in der Medizin findet die alte Einheit Torr auch heute noch häufig Verwendung.

Mit dem CSF im Hirnkammersystem und im Wirbelkanal des menschlichen Körpers verhält es sich kaum anders als mit der Druckverteilung in einem mit Wasser gefüllten Becher – mit einem entscheidenden Unterschied: Es gibt im menschlichen Körper keine "freie Oberfläche" mit bekanntem Atmosphärendruck.
Somit gleicht die CSF-Säule im Wirbelkanal des menschlichen Körpers bei näherem Hinsehen vielmehr einer verschlossenen, aufrecht stehenden Flasche im Schwerefeld der Erde, bei der die absoluten Druckverhältnisse, von außen betrachtet, unbekannt sind, wir aber Rückschlüsse über den Druckverlauf im CSF aus Analogien zu einfachen hydrostatischen Systemen ziehen können: der Druck nimmt von oben nach unten mit der Höhe der CSF-Säule stetig zu. Auch dieses Modell ist noch nicht ganz zutreffend - der menschliche Körper ist schließlich nicht starr. Für die hier vorgestellten hydrostatischen Phänomene ist dieser Detaillierungsgrad zunächst jedoch ausreichend.
Dass die Druckverhältnisse in realen hydrostatischen Systemen – wie z.B. näherungsweise im menschlichen Körper oder in einem Shunt – trotz der einfachen zugrundeliegenden Gesetzmäßigkeit (hydrostatische Grundgleichung) schnell kompliziert und verwirrend werden können, soll an folgendem Beispiel demonstriert werden:
In der Abbildung unten sehen wir acht auf den ersten Blick sehr ähnliche Röhren A – H in denen sich trotz der Ähnlichkeit grundverschiedene hydrostatische, teilweise auch hydrodynamische (d.h. das Wasser fließt) Zustände einstellen:

A In die starre Röhre A wurde eine Flüssigkeit mit dem Überdruck px hineingedrückt und das System dann sofort dicht verschlossen. Der Überdruck wird in der starren Röhre konserviert. Wäre die Röhre flexibel, würde sie sich wegen dem Überdruck px wie ein Ballon aufweiten. Im Stehen herrscht auf dem Boden der Röhre der Überdruck px plus der HD +10 cm.
B Röhre B ist oben offen und hat dort Kontakt zur Außenluft. Einen Überdruck px gibt es hier also nicht mehr. Deshalb herrscht oben definitionsgemäß 0 und unten auf dem Boden +10 cmH2O.
C Röhre C ist unten offen und oben geschlossen. Unten herrscht definitionsgemäß 0 cmH2O. Herausfließen kann das Wasser nicht, denn sonst entstünde wie bereits erwähnt oben ein Vakuum. Aber es versucht dies: die hängende Wassersäule zieht den oberen Deckel nach unten und erzeugt oben einen negativen hydrostatischen Druck von -10cmH2O, der auch Sog genannt wird.
D Röhre D ist identisch zu C, aber der Deckel ist nun etwas flexibel und zeigt deshalb deutlich die reale Existenz und die Auswirkung des Soges. Das ist wichtig, denn man sieht ja im wahrsten Sinne des Wortes „nichts“ bzw. „nichts fließen“ und der Sog ist somit eine reine Behauptung.
E Röhre E ist oben und unten offen und läuft deshalb einfach leer. Die treibende Kraft hinter diesem Vorgang ist einfach das Gewicht des Wassers, das nun ungehindert nach unten „fallen“ kann.
F In Röhre F liegt das Loch zur Außenluft mit DD 0 cmH2O genau in der Mitte. Herausfließen kann nichts, aber der HD unten beträgt nun wegen der geringeren hydrostatischen Höhe unten nur noch +5 cmH2O und der Sog oben -5 cmH2O.
G Röhre G hat oben wieder einen flexiblen Deckel, um die reale Existenz und die Auswirkung des Soges sichtbar zu machen. Auch der untere Deckel könnte flexibel sein und würde sich dann aufgrund des positiven Überdruckes nach außen wölben.
H In Röhre H fehlt der obere Deckel und die Röhre läuft deshalb zur Hälfte leer. Nur der positive HD von + 5 cmH2O auf dem Boden bleibt erhalten.
Es sei an dieser Stelle ganz besonders auf die Röhren (C) und (D) hingewiesen, die die Entstehung des sogenannten „Siphon-Effektes“ verdeutlichen. Dieser hat in der Shunt-Therapie eine besonders große Bedeutung. Der flüssigkeitsgefüllte Katheter, der bei einem Patienten mit Shunt von den Ventrikeln (geschlossenes Ende) in den Bauchraum (Peritoneum, offenes Ende) führt, stellt nämlich genau so ein hydrostatisches System dar, solange der Patient aufrecht steht. Der so erzeugte hohe Sog oben in den Ventrikeln ist physikalisch unvermeidlich und es bedarf spezieller Implantate, um ihn zu kompensieren.
Im Kern ist dieser Effekt auch dafür verantwortlich, dass beim gesunden Menschen der Hirndruck im Stehen leicht negativ ist: der Liquor sackt in dieser Position nämlich aus den Ventrikeln in den Spinalsack (in der Wirbelsäule) ab. Der Spinalsack ist zwar nicht unten offen, so wie die Röhre C & D, aber er ist recht flexibel und kann einigen Liquor zusätzlich aufnehmen. Zusätzlich führen ein paar weitere physiologische Mechanismen zum Glück dazu, dass der „physiologische“ (gesunde) Hirndruck im Stehen nicht auf –100 cmH2O abfällt, sondern nur auf circa -5 bis -15 cmH2O.
Würde eine der Röhren umfallen - oder legt sich ein Mensch sich hin - nimmt die Höhe der Wassersäule mit einem Mal ab und die Druckunterschiede zwischen zwei unterschiedlichen Orten - zum Beispiel Flaschenhals und Flaschenboden - werden im Schwerefeld der Erde nivelliert, sobald sie sich auf der gleichen hydrostatischen Höhe befinden.
Zusammengefasst heißt das also: In einem sehr groben Modell ist der Mensch für uns eine mit Hirnwasser gefüllte, aufrechtstehende Flasche im Schwerefeld der Erde. Der Flüssigkeitsdruck im Kopf ist in aufrechter Position aufgrund des hydrostatischen Drucks der Hirnwassersäule geringer als im Spinalkanal. Bei welchem Druck die Flasche einmal verschlossen worden ist, entzieht sich durch alleiniges "Hinschauen" unserer Erkenntnis.
Auf der Grundlage von solchen einfachen physikalischen Gedankenexperimenten - ausgehend von Bechern und Flaschen - kann man also erahnen, was mit dem Druck im CSF im Körper des Menschen geschieht, wenn er sich neigt, beugt oder hinlegt: Der hydrostatische Druck im CSF ist an verschiedenen Orten im menschlichen Körper nicht konstant sondern "passt sich" der Lage und Aktivität des menschlichen Körpers "an".
Die Annahme, dass die Druck-Verhältnisse im menschlichen Körper ausschließlich mit Hilfe der Hydrostatik beschrieben werden können, verhelfen uns zu einem grundlegenden und häufig auch schon ausreichend guten Verständnis der Phänomene, die wir beobachten bzw. messen können. Dies kann für die Behandlung des Hydrocephalus, z.B. bei der Vermeidung von Überdrainage, von großer Bedeutung sein.
Es handelt sich jedoch dennoch um eine starke Vereinfachung der tatsächlichen, hoch komplexen Gegebenheiten im menschlichen Körper. Schließlich wird CSF im Gehirn aus dem Blut produziert und wieder absorbiert. Es gibt also Quellen und Senken und somit notwendigerweise einen - wenn auch langsamen - Fluss. Durch das Pulsieren der Arterien im Inneren der Hirnventrikel und nach jüngsten Forschungen auch maßgeblich durch die Atembewegungen des menschlichen Körpers zirkuliert das CSF im Hirnventrikelsystem. Mittels moderner fluss-sensitiver Echtzeit-MRT-Aufnahmen des menschlichen Schädels lassen sich diese Zirkulationen sogar eindrücklich nachweisen (Dreha-Kulaczewski1, 2017).
Hydrodynamik im Shunt
Wird das Hirnventrikelsystem durch einen Shunt "gestört", wird diese Strömung manifest: Die Druckdifferenz zwischen den Ventrikeln und dem Peritoneum ermöglicht eine "Netto-Strömung" des CSF in das Peritoneum durch den künstlich geschaffenen Kanal, der mittels spezieller Differenzdruck- bzw. hydrostatischer Ventile reguliert wird. Da eine Strömung bei konstanter Flüssigkeitsproduktion, gemäß der Kontinuitätsgleichung der Hydrodynamik, schneller fließt, je enger der durchströmte Flusskanal ist, wird die Flüssigkeit im vergleichsweisen engen Katheter schneller fließen als zum Beispiel durch ein Reservoir mit deutlich größerem Flussquerschnitt. Werden beispielsweise 20 ml CSF pro Stunde abgeleitet, fließt das CSF mit immerhin 5 Millimetern pro Sekunde durch den Katheter. Die Flussgeschwindigkeit nimmt jedoch im gleichen Maße ab in dem sich der durchflossene Querschnitt vergrößert.
Kontinuitätsgleichung
Die Kontinuitätsgleichung ist eine der Grundgleichungen der Hydrodynamik und lässt sich als eine einfache Massenbilanz um ein Kontrollvolumen auslegen. Dabei gilt vereinfacht gesagt: „Was rein geht, muss auch wieder raus“. Sie lässt sich recht anschaulich und ohne viel physikalisch-mathematisches Grundwissen aus den folgenden Axiomen herleiten:
- (Masse/Zeit)_rein = (Masse/Zeit)_raus
- Masse=Dichte*Volumen. // Annahme: Die Dichte ist konstant.
Aus 1. in 2. folgt: (Volumen/Zeit)_rein = (Volumen/Zeit)_raus
<-> ((Fläche) * (Strecke/Zeit))_rein = ((Fläche) * (Strecke/Zeit))_raus // Geschwindigkeit = Strecke / Zeit mit Volumen = Fläche * Strecke
Daraus folgt:
V_rein*A_rein = V_raus*A_raus

Einige kennen es vielleicht vom Kanufahren durch engere Kanäle: Je enger der Kanal, desto schneller schwimmt das Kanu mit der Strömung mit.
Wird die CSF-Flussgeschwindigkeit nun durch den potentiell vergrößerten Querschnitt eines Hydrocephalusventils gedrosselt, kann - begünstigt durch Verwirbelungen und Staupunkte an unregelmäßigen Geometrien mit nahezu stillstehendem Liquor, die Interaktionen und Anhaftungen der im Liquor enthaltenen Gewebeteilchen, Proteine und manchmal auch Blut mit den Oberflächen im Inneren der Ventile durch längere Expositionszeiten sukzessive zu einer Okklusion des Ventils führen.
"... found in relation to toxicity and oncogenity. Minor problems existed in relation to CSF proteins and medium difficulties in relation to corpuscles (blood). Surprisingly with 500 mg/dl protein, most valves showed – in short term – no significant alteration except of some sticking proximal slit probes and sometimes Orbis-Sigma valves. The trials of Brydon et al. (1996) could be confirmed. Protein effects are usually overestimated. Corpuscles and blood are more by far at risk for valve occlusions (Aschoff 1995)." Aschoff2, 2019
Das Verständnis über die genauen Mechanismen von Ventilokklusionen auf molekularer Ebene sind bedeutend für den langfristigen Erfolg eines Shunts und daher auch aktueller Gegenstand von wissenschaftlichen Untersuchungen. Immer noch wissen wir recht wenig über die Hintergründe zur Entstehung von Verstopfungen. Wir ahnen jedoch: Die Berücksichtigung der Strömungsgeschwindigkeit ist vermutlich von großer Bedeutung bei der Auslegung von Shuntsystemen.
Geräusche im Ventil
Nicht nur in Bezug auf Okklusionen kann die Strömungsgeschwindigkeit durch den Shunt von Bedeutung sein. Auch die Entstehung von Ventilgeräuschen – wie sie von Hydrocephaluspatienten in manchen Fällen berichtet werden (Kästner3, 2017) – lässt sich mit Hilfe von Phänomenen, die mit der Flussgeschwindigkeit des CSF zusammenhängen, erklären.
Anhand eines einfachen Differenzdruckventils verdeutlicht - z.B. anhand eines Kugel-Konus-Ventils - wird der Druck im Shunt proximal solange aufgebaut, bis er die Kraft des Federelements im Ventil überwinden kann. Wenn die aus dem Druck resultierende Kraft auf die Kugel schließlich die Federkraft überwindet, bewegt sich die Kugel, öffnet so den Flusskanal und das Fluid kann sich in Bewegung setzen.
Unter bestimmten Bedingungen kann es nun dazu kommen, dass sich das Ventil unmittelbar nach dem Öffnen infolge eines plötzlichen Druckabfalls im CSF wieder schließt. Verantwortlich für diesen besonders raschen Druckabfall ist einerseits der Druckabbau auf der Überdruckseite durch das Abführen der Flüssigkeit. Dieser kann je nach konkreter Anatomie (z.B. Hirncompliance, Schlitzventrikel etc. ) sehr schnell vonstatten gehen. Hinzu kommt ein weiterer Druckabfall, der durch die sogenannte Bernoulli-Gleichung beschrieben wird, welche besagt, dass der Druck in einem Fluid, das sich in Bewegung setzt, geringer ist als in einem ruhenden Fluid. Für das Ventil heißt das konkret: je schneller CSF durch das geöffnete Ventil fließt, um so größer der nachfolgende Druckabfall und um so größer die Tendenz zum schnellen Wieder-Schließen.
Bernoulli-Gleichung
Die Bernoulli-Gleichung ist jedem, der sich mit Strömungslehre beschäftigt, ein Begriff, da sie häufig einen ersten Einblick in die Gegebenheiten von ansonsten komplexen, hydraulischen Systemen ermöglicht. Es handelt sich dabei letztlich um eine Variante des Energieerhaltungssatzes, welche besagt, dass entlang einer Stromlinie die Summe aus potentieller Energiedichte (hydrostatische Wassersäule), kinetischer Energiedichte und Energiedichte der im Fluid wirkenden inneren Kräfte (statischer Druck) stets konstant bleibt:
Spez. Potentielle Energie + Spez. Kinetische Energie + Spez. Innere Energie = const.
rho g h + ½ rho v² + p = const.
Streng genommen gilt sie nur für homogene Strömungen. Das sind idealisierte, real also nichtexistierende Strömungen die stationär (keine lokalen Geschwindigkeitsänderungen), inkompressibel und frei von Druckverlusten sind. Es existieren aber auch Formulierungen der Bernoulli-Gleichung, die Druckverluste durch Turbulenzen oder Rohrreibung durch einen zusätzlichen Term berücksichtigen.
Eine Konsequenz dieser Gleichung ist, dass der innere oder auch „statische“ Druck einer Flüssigkeit umso geringer ist, je schneller das Fluid sich bewegt. Dies wird häufig anschaulich am Beispiel der sogenannten Venturidüse demonstriert, die hier schematisch aufgezeichnet ist:

Während die Geschwindigkeit der Strömung im engsten Querschnitt am höchsten ist (vgl. Konti-Gleichung), ist der innere Druck der Strömung dort am geringsten, wodurch sich die Flüssigkeitssäule im abgebildeten U-Rohr-Manometer in gezeigter Weise verschiebt.
Da sich der Druck daraufhin sofort wiederaufbauen kann, kommt es so zu einem wiederholten Öffnen und Schließen des Ventils – und dabei auch zu hörbaren Geräuschen.
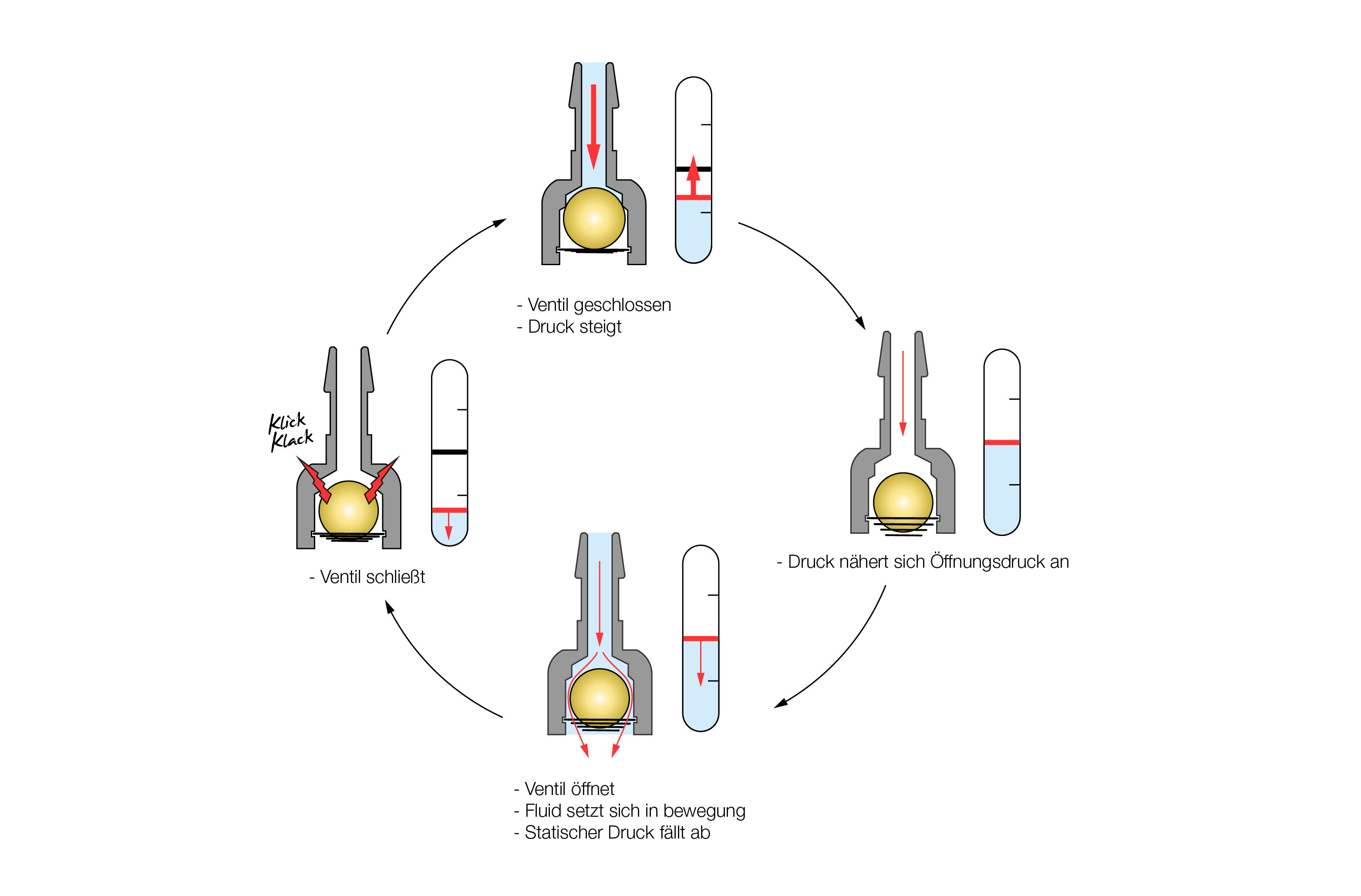
Dieses Phänomen lässt sich auch experimentell belegen, wie in folgendem Video zu sehen ist:
Wir sehen also: Obwohl sich grundlegende Phänomene von Hirndruck und Hydrocephalustherapie mit einfachen, hydrostatischen Modellen beschreiben lassen, kommt man nicht umhin, sich auch hydrodynamischer Modelle zu bedienen, um die Fluidmechanik und ihre Auswirkungen im Shunt verstehen zu können.
Damit sind längst nicht alle Fragen von Hydrostatik und Hydrodynamik in Shuntsystemen beantwortet. Ich freue mich auf Anregungen oder Fragen, die wir in anderen Artikeln intensiver aufgreifen können.
Zum Abschluss - und um die Komplexität noch ein bisschen zu unterstreichen - die "simple" physikalische Antwort auf eine uns oft gestellte Frage, warum die Öffnungsdrücke von in Reihen geschalteten Ventilen addiert werden müssen:
1 + 1 = 1? Oder: Addition von Öffnungdrücken von in Reihe geschalteten Ventilen
Die Bilanzgleichungen der Fluidmechnik können auch helfen, ein beliebtes Missverständnisse in Bezug auf die Kombination von Hydrocephalusventilen, speziell: der Reihenschaltung von Ventilen mit unterschiedlichen Öffnungsdrücken zu klären: Addieren sich die einzelnen Öffnungsdrücke wirklich oder steuert nicht doch etwa der höhere Öffnungsdruck als der dominantere von beiden den CSF-Fluss durch den Shunt steuert?
Mit Bezug auf die hydrodynamischen Bilanzgleichungen und etwas Vertrauen in die theoretische Physik kann diese Frage auch ohne Experiment beantwortet werden. Hierzu genügt eine einfache Impuls- oder - im hydrostatischen Grenzfall - auch Kräftebilanz, um das Kontrollvolumen „CSF-Säule im Shunt“. Unter Berücksichtigung der Tatsache, dass es sich bei der betrachteten Flüssigkeitssäule um ein sogenanntes Kontinuum handelt und jede Masse im Inneren der Flüssigkeit einen Druck auf die Grenzen des Kontrollvolumens bedeuten, wird deutlich, dass die einzelnen Massen nicht separat sondern summiert in die Bilanzgleichung einfließen.
Oder einfacher, weniger kurz und weniger abstrakt gezeigt:
Stellen wir uns zwei einfache Kugel-Konus-Ventile mit zwei verschiedenen Federn (blau) hintereinander in Serie vor:
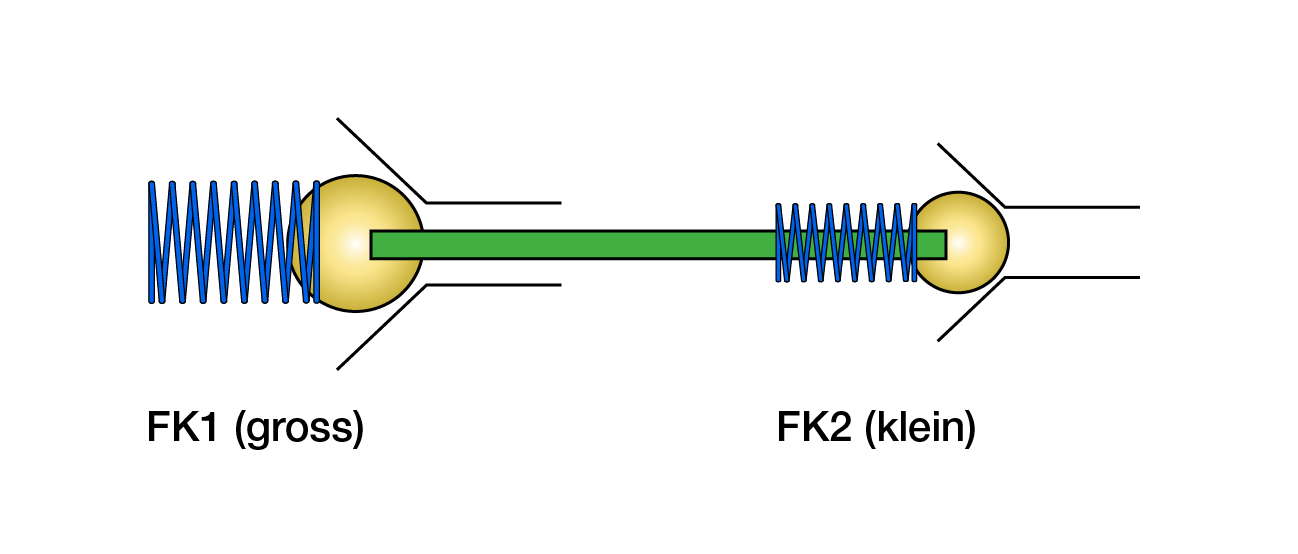 Die blauen Federn haben verschiedene Federkonstanten - klein (FK2) und groß (FK 1). Das Flüssigkeitsmedium dazwischen ist inkompressibel und kann daher - gedanklich - durch z.B. ein Stahlstange (grün) ersetzt werden, die beide miteinander verbindet und so direkt die Kraft überträgt. Jetzt wird deutlich, dass man das Gesamtsystem nur öffnen kann, wenn auf die Stahlstange (oder in der Realität: auf das Wassermedium) mit einer Kraft gedrückt wird, die die Summe aus BEIDEN FEDERKONSTANTEN FK1 + FK2 kompensiert - das ist mit Kräftebilanz gemeint.
Die blauen Federn haben verschiedene Federkonstanten - klein (FK2) und groß (FK 1). Das Flüssigkeitsmedium dazwischen ist inkompressibel und kann daher - gedanklich - durch z.B. ein Stahlstange (grün) ersetzt werden, die beide miteinander verbindet und so direkt die Kraft überträgt. Jetzt wird deutlich, dass man das Gesamtsystem nur öffnen kann, wenn auf die Stahlstange (oder in der Realität: auf das Wassermedium) mit einer Kraft gedrückt wird, die die Summe aus BEIDEN FEDERKONSTANTEN FK1 + FK2 kompensiert - das ist mit Kräftebilanz gemeint.
Literaturverzeichnis
Dreha-Kulaczewski 2017: Inspiration is the major regulator of human CSF flow
Aschoff 2019: in In-Depth View — Functional Characteristics of CSF Shunt Devices (Pros and Cons)
Kästner 2017: I can hear my shunt — audible noises associated with CSF shunts in hydrocephalic patients



